
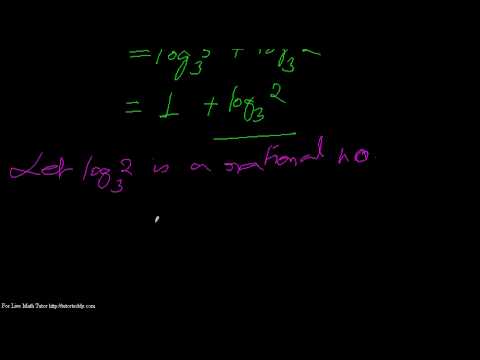

One can also replace Log a by other logarithms of a to obtain other values of a b, differing by factors of the form e 2inb. Namely, if a and b are complex numbers with a 0, one can use the principal value to define a b e b Log a.
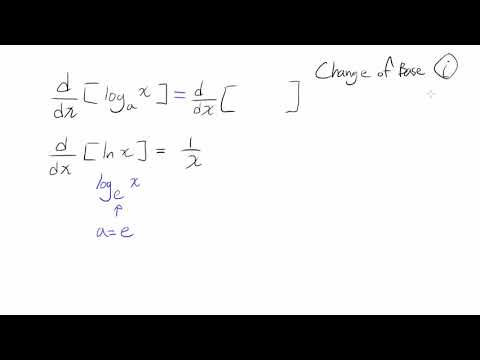
A useful mathematical differentiation calculator to simplify the functions. The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8). The complex logarithm is needed to define exponentiation in which the base is a complex number. Similarly, what is the derivative of log base 2 Calculus Examples The derivative of log2(x) log 2 ( x ) with respect to x is 1xln(2) 1 x ln ( 2 ). This derivative can be found using both the definition of the derivative and a calculator.

Ensure that the input string is as per the rules specified above.Īn online derivative calculator that differentiates a given function with respect to a given variable by using analytical differentiation. The derivative of the natural logarithmic function (lnx) is simply 1 divided by x. Use inv to specify inverse and ln to specify natural log respectivelyĦ. Write sinx+cosx+tanx as sin(x)+cos(x)+tan(x)Ĥ. Use paranthesis() while performing arithmetic operations.Įg:1. Use ^(1/2) for square root ,'*' for multiplication, '/' for division, '+' for addition, '-' for subtraction.ģ. As the logarithmic function with base, and exponential function with the same base form a pair of mutually inverse functions, the derivative of the logarithmic. (In fact, these properties are why we call these functions “natural” in the first place!)įrom these, we can use the identities given previously, especially the base-change formula, to find derivatives for most any logarithmic or exponential function.2. Look at some of the basic ways we can manipulate logarithmic functions: From the properties of logarithms (logba logca / logcb), 10log96 can be rewritten as 10(log36. This means that there is a “duality” to the properties of logarithmic and exponential functions. Find integer solutions for m - n(log3(2)) 10(log9(6)). Take a moment to look over that and make sure you understand how the log and exponential functions are opposites of each other. 1 To differentiate logarithmic functions with bases other thane, use logb m lnm lnb Example Find the derivative of y log2(5x3). In general, the logarithm to base b, written \(\log_b x\), is the inverse of the function \(f(x)=b^x\). Therefore, the natural logarithm of x is defined as the inverse of the natural exponential function: By the Sum Rule, the derivative of x 2 3 x x 2 - 3 x with respect to x x is d d x x 2 + d d x 3 x d d x x 2 + d d x - 3 x. Replace all occurrences of u u with x 2 3 x x 2 - 3 x. For example log base 10 of 100 is 2, because 10 to the second power is 100. The derivative of log 3 ( u) log 3 ( u) with respect to u u is 1 u ln ( 3) 1 u ln ( 3). When we take the logarithm of a number, the answer is the exponent required to raise the base of the logarithm (often 10 or e) to the original number. Overview Derivatives of logs: The derivative of the natural log is: (lnx)0 1 x and the derivative of the log base bis: (log b x) 0 1 lnb 1 x Log Laws: Though you probably learned these in high school, you may have forgotten them because you didn’t use them very much. Remember that a logarithm is the inverse of an exponential. 3.6 Derivatives of Logarithmic Functions Math 1271, TA: Amy DeCelles 1. We'll see one reason why this constant is important later on. Laws of Logarithms Three laws of logarithms may be expressed as: (i) log(A ×B)logA+logB (ii) log A B logA logB (iii) logAn nlogA In calculus, Napierian logarithms (i.e. This equation involves the log base 10, so we apply the inverse function. The natural exponential function is defined as cients of logarithmic functions, and (iii) the differ-entiation of implicit functions. Review of Logarithms and Exponentialsįirst, let's clarify what we mean by the natural logarithm and natural exponential function. While there are whole families of logarithmic and exponential functions, there are two in particular that are very special: the natural logarithm and natural exponential function.
DERIVATIVE OF LOG BASE 3 HOW TO
In this lesson, we'll see how to differentiate logarithmic and exponential functions. Differentiating a Logarithm or Exponentialīy now, you've seen how to differentiate simple polynomial functions, and perhaps a few other special functions (like trigonometric functions).


 0 kommentar(er)
0 kommentar(er)
